The following information on getting power from a stream comes from Five Acres and Independence by M. G. Kains. Five Acres and Independence is also available to purchase in print.
Many a small stream, if harnessed, would furnish power enough to generate electricity for lights and small household appliances. Factors which determine the power a stream can develop, writes W. H. Sheldon,* are height of dam, and quantity of water flow. The height is limited by the height of the banks. It may be measured by using a carpenter’s level and a rule. The quantity of water flowing may be determined by means of a weir dam (Fig. 7-A). [*Quarterly bulletin of the Michigan Experiment Station (Vol. XIV, No. 1.)
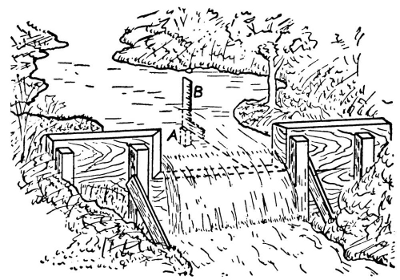
The weir consists of a rectangular notch cut in a temporary dam across the stream. The notch should be centered and its width not more than 2/3 that of the dam, but sufficiently wide, so the water flowing over the lip will be not more than 10″ nor less than 1″ deep. This depth of water should not be more than 1/2 the drop outside. The edges of the notch should be beveled on the sides and the bottom (Fig. 8-A) to afford as little resistance as possible to the flow. It is essential that the dam be high enough so the water will be quiet before reaching the weir and that the weir be wide enough so the flow will not be too rapid.
As the water surface above the dam slopes toward the notch the depth of the water flowing over the weir must be measured up-stream. To do this set a stake (A) 4′ back of the weir with its top exactly level with the lip of the weir. An ordinary rule (B) set on this stake will measure the depth of water flowing over the lip. The depth of the water being known the volume of the flow is determined from the formula Q=3×w×d÷d. Q equals discharge in gallons a minute; w, width of notch in inches; d, depth in inches flowing over weir.
Having determined the gallons a minute and the available head in feet, the power that may be developed is: H.P.=(Q×H)÷4,000. Q equals gallons a minute and H, available head in feet.
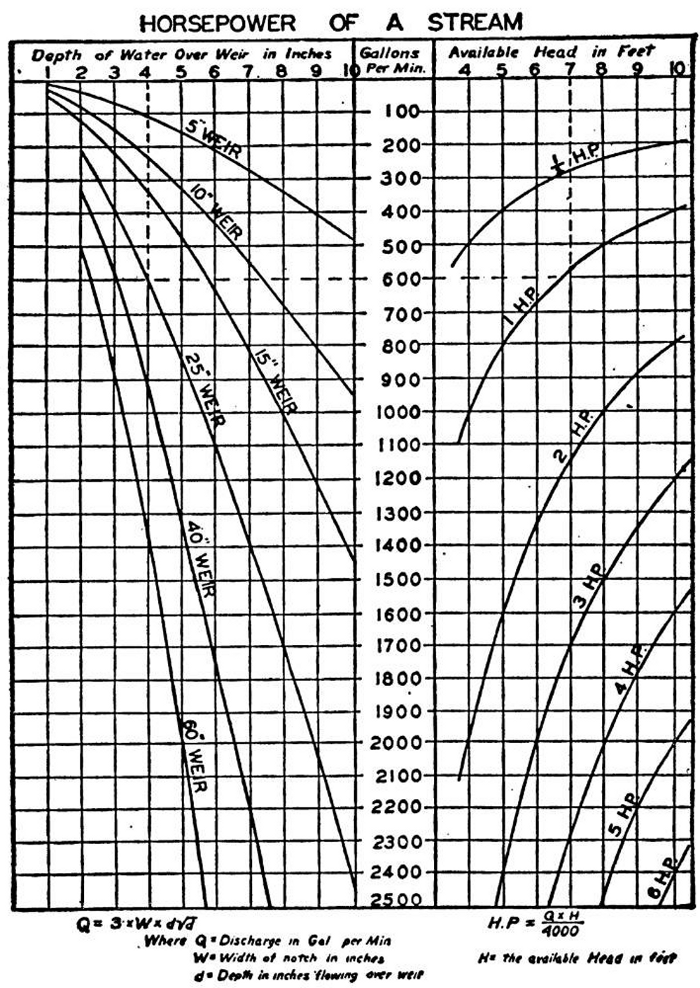
The width of the weir, depth of water flowing over it and the available head being known the horse-power may be read directly from the graph (Fig. 9-A). Example: If a weir notch is 25″ wide and 4″ of water flows over it what power will the stream develop with a 7′ dam? By the formula:
Q=3×25×4÷4=600 gallons a minute
H.P.=(600 gal.×7 ft.)÷4,000=105 H.P.
Turning to the graph (Fig. 9-A) follow the curve near the left side marked 25″ weir to intersection of vertical line under 4″ Water Depth. On a horizontal to the right of this intersection, find the quantity 600 gallons a minute in the center column. Follow the same horizontal line to the right until it intersects the vertical line under 7′ of head which is just to the right of the curve marked 1 H.P. This indicates that the stream will develop slightly more than 1 H.P.
1. With a given depth the amount of water flowing over the weir is proportional to the length of the weir. 2. With a given fall the power a stream will develop is proportional to the quantity of water available. 3. With a given quantity of water, the power a stream will develop is proportional to the fall used.
Streams that develop four horse-power or more will operate a lighting plant without a storage battery by using a turbine with a generator which will deliver a constant voltage. Smaller streams which develop at least one horse-power will operate battery-charging light plants satisfactorily, but those which develop less than one horse-power are better for operating hydraulic rams for pumping water. It is usually not advisable to attempt to harness a stream unless the dam can be built at least 4′ high because a special, large capacity turbine or undershot wheel would be required to develop even a small amount of power.
After determining that a stream will develop ample power, the expense of harnessing it should be carefully considered; for instance, the location of the dam site should be reasonably near the buildings where the electricity will be used in order to avoid the necessity of a long transmission line. If the banks are widely separated, a long dam will be required and a large area will be inundated, or if the banks are very porous a dam that will hold back the water will be costly to build.
